Research.ganse.org

LONG-RANGE OCEAN ACOUSTIC SCATTERING
In 2009 and 2010 I participated in a major ocean acoustics experiment in the Philippine Sea with APL-UW's North Pacific Acoustic Laboratory (NPAL) group. One of the key topics our research group is interested in is how oceanic sound propagation is affected by internal waves (waves down deep in the water) and by ocean "spice" (blobs of water with a different soundspeed but same density as their surroundings, so they don't behave like waves). Both these phenomena cause variations in soundspeed of the water and thus acoustic transmissions through it, and acousticians would like to understand them better. Our group is also interested in the estimation of ocean sound-speeds and temperatures from receptions of sound that we send through the water. Find out more about our use of these different methodologies in our research on my NPAL Ocean Acoustics page.


RADIO SCIENCE GRAVITY INVERSION FOR ICY MOON INTERNAL STRUCTURE
The nature of an icy satellite's interior relates fundamentally to its composition, thermal structure, formation and evolution history, and prospects for supporting life. Gravity measurements via radio Doppler information during spacecraft flybys are an important tool used to infer gross interior structure of these moons. Liquid water and ice layers have previously been inferred for the interiors of Jupiter's icy satellites Europa, Ganymede, and Callisto on the basis of magnetic field measurements by the Galileo probe, and on Europa and Callisto induced magnetic field signatures measured by the Galileo probe provided strong evidence for an ionic aqueous ocean. We apply geophysical inverse theory tools to assess the icy moon's interior density anomaly distribution that could be estimated from radio Doppler measurements, to support the search for mass anomalies in the ice shell (meteorites or diapiric upwellings) or near the H2O/rock interface (seamounts).


INTRODUCTORY BEAMFORMING TUTORIAL
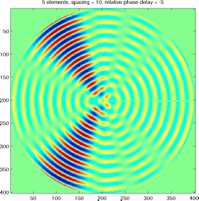Using beamforming you can direct the majority of signal energy you transmit from a group of transducers (like audio speakers or radio antennae) in a chosen angular direction. Or you can calibrate your group of transducers when receiving signals such that you predominantly receive from a chosen angular direction. Here's a simple, introductory tutorial demonstrating the phenomenon using Matlab scripts to superimpose waves emanating from an array of sources.


RAYTRACING JAVA APPLETS!
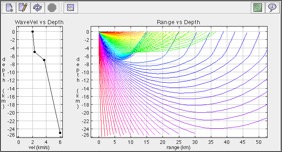
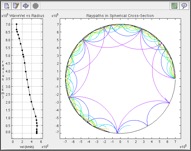Raytracing is a high-frequency approximation to the propagation of waves in a medium, and it makes pretty cool animated plots. We specify a set of rays, normal to the wavefronts, and we can set properties of the environment like dimensions and wavespeeds, and then we can watch where the wave energy goes by watching where the rays go. If the wave velocity is a non-constant function of location in the medium then these then rays will curve, sometimes overlapping each other, sometimes leaving wide gaps in where they return to the surface. This raytracing approach can be used for seismic waves in the Earth, for acoustic waves in the ocean (an "ocean" option will be available before too long on this applet), and even for ion-acoustic waves traveling through the Sun - I've both Cartesian and Polar versions of this Java applet on here to play with (click respective graphic to go to either).

ELECTROMAGNETIC INVERSION OF ESTUARINE SALINITY STRUCTURE USING SMALL-SCALE CSEM
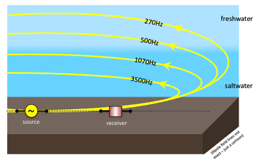The Conductivity Profiler is an instrument for remotely observing estuarine salinity profiles via electromagnetic measurements. Electromagnetic (EM) waves are attenuated in seawater as a function of frequency, and conductivity structure (closely related to salinity structure) in the water can be inferred by combining measurements of EM waves at different frequencies on a distant electric field receiver. Geophysical inversion methods are applied to estimate the estuarine salinity profile from the EM measurements. Using inverse theory techniques, we take advantage of statistical rigor and let the data determine the structure of the conductivity profile and quantify the uncertainty and resolution of the salinity profile.


GEOACOUSTIC INVERSION (my PhD topic)
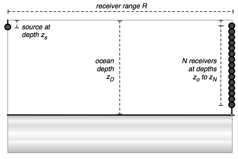The Navy’s engineering interest in improving sonar performance in shallow waters is dependent upon an understanding of features and properties in the ocean subfloor which interact with the sonar acoustics. This need in turn drives the geophysical science goal of understanding the nonlinear inversion of ocean bottom properties from hydrophone-based measurements given an acoustic source in the water, within the context of typical naval equipment and frequencies. The geoacoustic inverse problem is closely related to terrestrial seismic inversion and certainly to marine seismic inversion, but at different frequencies and size scales than typically used in seismology and oil exploration work. While specific formulations vary across the field of geoacoustic inversion, the overall problem is to estimate the ocean bottom properties as a function of position in the top few hundred meters of the ocean bottom, given finite measurements of acoustic pressure from arrays of hydrophones located in the water column. My PhD in this work studied the geoacoustic inverse problem at a theoretical and computational level, with goals of obtaining the most information possible out of the measured data without imposing preconceived notions of what the solution should be, and of providing tools to plan new geoacoustic experiments that seek to obtain the most informative data possible for the problem.


PREDICTIVE FILTERS COMPARISON
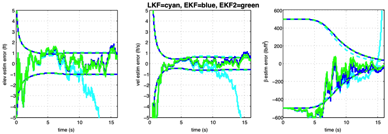
A classic textbook for predictive (tracking) filters is Applied Optimal Estimation, edited by Gelb (1974). In section 6.1 of that book are two simple radar tracking examples (6.1-2 and 6.1-3) which demonstrate several nonlinear filters. I've programmed up those examples into a Matlab script and added a few additional filters to compare and contrast them in both linear and nonlinear cases.





InvGN: GAUSS-NEWTON NONLINEAR INVERSION CODE
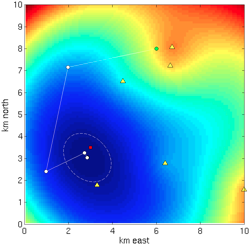Calculate Tikhonov-regularized, Gauss-Newton nonlinear iterated inversion to solve the damped nonlinear least squares problem, using the InvGN toolkit for Matlab/Octave. While Matlab's optimization toolbox contains lsqnonlin, it does not inherently include the Tikhonov regularization and is only the optimization component, whereas inversion also requires uncertainty quantification. My InvGN package is for weakly nonlinear, Tikhonov-regularized, inverse problems (so includes solution uncertainties and resolution quantification), handles both frequentist and Bayesian frameworks, and also works in Octave.