FLOW_MODELS: IMAGE GENERATION AND ANOMALY DETECTION AS TWO SIDES OF SAME COIN.
Normalizing flow models are invertible neural networks, a type of generative model that offers a nice two-for-one benefit: simultaneously enabling unsupervised learning for image anomaly detection (by mapping unlabeled images to a distribution where statistical anomaly detection techniques can apply) and also enabling image simulation (by mapping randomly generated samples from a probability distribution into the image space). Now it may not be my ultimate use case, but it turns out there are, you know, a ton of cat images and datasets on the internet, so let's experiment with INNs and cats!VIM-MLFLOW PLUGIN TO BROWSE MLFLOW RESULTS IN VIM
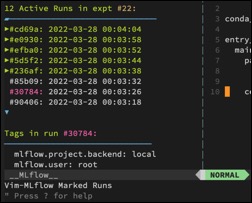I love MLflow a lot, and I use it all the time for both work and personal projects. There are projects in which I go all-out and auto-log extensive graphical artifacts to better enable modeling improvements - like with example images for the different error cases, and ROC curves, and so on. And for those it's really nice to use its website as a one-stop UI to where those artifacts are logged and reviewed by others. But there are also a lot of projects where I really don't log much more than the modeling parameters and performance metrics, just numbers, and yet I'm still leaving my terminal-based workflow in Vim and looking up and comparing those numbers on the (in this case needlessly point-and-click) MLflow website. So I wrote this Vim plugin...PREDICTING BANK LOAN BEHAVIOR WITH RANDOM FOREST MODELS
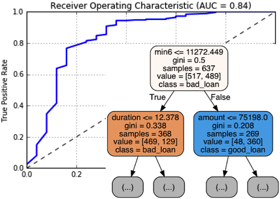Let's implement a random forest classifier from Scikit-Learn to see how well we can predict whether a bank client will have good loan behavior (meaning they won't default or become delinquent) if they are given a new loan. We'll use a public bank transactions/loans dataset from the PKDD99 Challenge conference for the modeling. In the process we'll fit and explore the assumptions made for this model, and learn about some limitations of Scikit-Learn's tree-based models.POSTGRESQL+SCHEMASPY VIA DOCKER CONTAINERS
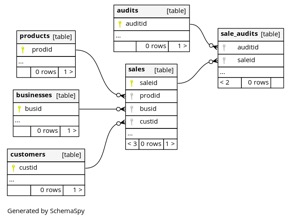When prototyping a new database from its initializing SQL code, and wanting to examine details of its relational architecture or demonstrate it to others, it's really convenient to simply pull my aganse/quick_postgresql repo. I just pop in my table creation lines in init.sql, make run, and view the interactive SchemaSpy website generated at its internal port. As the database sticks around and grows into use, still it's really helpful as it evolves to be able to keep rerunning and updating that SchemaSpy website as a standard part of the workgroup toolset.MEDICAL IMAGE CLASSIFICATION BUILT WITH "MLFLOW PROJECTS"
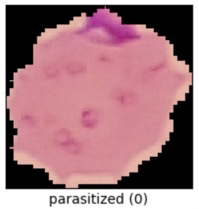Let's explore a supervised learning problem in medical imaging based on a public dataset and MLFlow's "Projects" functionality. A self-contained modeling module is trained, has its performance logged in MLFlow, and is able to be checked out as a deployable model image. There's a configurable implementation of this in my aganse/py_tf2_gpu_dock_mlflow repo. Let's try the malaria detection dataset from the Tensorflow datasets, which contains a balanced, labeled dataset of about 27,000 thin blood smear slide images of cells, and let's see how well we can detect malaria parasite presence in the images. This dataset is used to train/test different variations of image classification models, including VGG-16 and various sizes of more basic convolutional networks.GPT_CLIENT CLI WITH PARAMETER CONTROL, WEBLINK SUBMISSION, & SYNTAX HIGHLIGHTING
I have found OpenAI's GPT models to be fabulously productive tools and use them often in my technical work now. But to get what I want out of the models for my uses has taken accessing the models from the API rather than the ChatGPT website GUI.
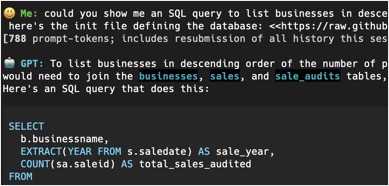This allows me to change some of the model parameters, format the output as I wish, and run the whole thing in my terminal. Of course the process of making the app has provided highly useful education in understanding how the models work as well, including how interacting with them via API can enable no end of use cases from other automated code.DBSCAN CLUSTERING IN DECRYPTING AN IMAGE CYPHER
This wonderful kids' book series is fun not only for the stories themselves, but also because each of the first several books involves a cipher puzzle with "fairy hieroglyphics" - I love code puzzles! In the electronic form of the books I discovered the hieroglyphic sequence was moved to the back of the book, all perfectly lined up in matrices over a few pages at the end. And I thought, hey that seems like it'd be easy to parse and decrypt on a computer, just like the main character did!INTERACTIVE GPS DATA VISUALIZATIONS IN PYTHON/JUPYTER
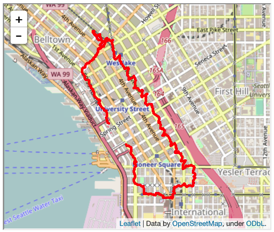Did you know you can plot your geographic data on interactive maps embedded directly in your Python notebooks? Check it out, as we play with and analyze some GPS tracking data. A database of tracked walking routes data available on a health/fitness website provides a convenient trove of data not only to play with, but also to explore the geometric interference effects of downtown buildings upon GPS track solutions.GETTING MLFLOW+DATABASE RUNNING QUICKLY VIA DOCKER
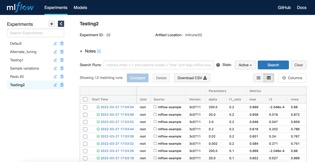This provides a get-running-quickly Docker-compose setup using containers for MLflow, PostgreSQL, and NGINX. Run MLflow's database in PostgreSQL, and put an NGINX reverse proxy in front of the MLflow website to allow some level of access restriction (say for a workgroup within an already-firewalled company intranet).