(This was a neat grad-school class project applying our continuum mechanics studies, UW Geophys 501, Autumn 2001)
PROPOSAL
Numerical Modeling to Verify the Linear Diapir Hypothesis for the Formation of Ice Double-Ridges on Europa
Andy Ganse, APL-UW, 18 Dec 2001
Introduction & Background
I propose to develop and explore a numerical model to further investigate the linear diapir hypothesis described in Head et al. 1999, for the formation of the ice double-ridges on Europa, one of the moons of Jupiter. This model will be compared to actual 3D data of Europan ridges estimated from photoclinometry as part of the evaluation of the model. Ideally the results will offer quantitative evidence to support or reject the linear diapir hypothesis, described only qualitatively in the above article, and provide constraints on the thickness of the ice layers covering the suspected ocean on Europa. Also, I hope that it will serve as a catalyst for similar modeling to explore the several other double-ridge formation hypotheses (see Pappalardo et al. 1999).
Europa is one of the four largest satellites of Jupiter, called the Galilean satellites (discovered by Galileo in 1610). Spectroscopy shows that Europa's bright white surface is predominantly water ice, and orbital and gravitational measurements yield a density profile of the moon in which an iron core and silicate mantle are enveloped by a 100km thick surface layer of water (Anderson et al. 1998). From telescopes and space probe photos it is visually clear that the outer, exposed surface of this water layer is frozen. But because the various phases of water all have similar densities it is not clear at this point whether the entire 100km water layer consists of ice (and of what phase), liquid water, or some combination of these. It is the hint of an immense liquid water ocean on a world besides Earth, and the possibility of extraterrestrial life in that ocean, which entices many scientists in the exploration of Europa. A Europa-specific orbiter and a landing probe are planned for the indeterminate future; in the meantime we are relegated to analyzing photos and spectral and magnetic measurements for clues about the structure and formation of the surface water layer. Investigating surface features such as these double ridges is interesting in its own right, but in particular it contributes to the indirect exploration of Europa's interior and hence the search for a Europan ocean and the possibility of extraterrestrial lifeforms.
Photos returned from the Voyager space probes in the 1970's and the Galileo space probe in the 1990's through the present show numerous large cracks in Europa's surface ice bounded with large ridges on either side (Figure 1). These ice cracks are arguably the largest and most noticeable feature on the surface of Europa, significantly larger than ice cracks or ridges on Earth (some as large as 300m high and 2.6km wide), and this double-ridge shape is rarely found on Earth. Consequently these Europan ice ridges have inspired a number of hypotheses about processes which form them and about how these processes constrain the thickness of the surface ice of Europa.

Figure 1. Picture PIA00589 of Europan ice ridges from the JPL Planetary Photojournal Database. This photo, taken from the Galileo space probe in 1997, shows an area of about 14 kilometers by 17 kilometers. The main ridge in the picture is approximately 2.6 kilometers wide and 300 meters high. (Courtesy of NASA/JPL/Caltech.)
Existing hypotheses for processes forming the double-ridges include the following (Pappalardo et al. 1999):
1.) Volcanism, in which liquid water is explosively ejected through fractures and repeatedly deposited in growing linear debris piles along the fractures.
2.) Tidal squeezing, in which liquid water or warmer ice from below is racheted up through tidal stress fractures in the surface layer of cold, brittle ice during each tidal cycle to form growing linear debris piles along the fractures.
3.) Linear diapirism, in which frictional heating from a tidal stress fracture causes an increased buoyancy in a warmer, ductile layer of ice below. This pushes up the cold, brittle, surface ice on either side along the length of the fracture resulting in tilted slabs that form current double ridge shapes after mass wasting.
4.) Compression, in which tidal compression deforms a warmer, ductile layer of ice below more than the cold, brittle, surface ice. This pushes up the surface ice along the length of a fracture, resulting in tilted slabs that form current double ridge shapes after mass wasting.
5.) Wedging, in which liquid water from below flows into tidal stress fracture, freezes, and creates a wedge against which tidal compression pushes, deforming the surface ice upward and outward into double ridges along the fracture.
These hypotheses involved little or no numerical work and some of the authors have even suggested that numerical modeling needs to be done to help substantiate or discredit the hypotheses. The aim of this proposal is to conduct numerical modeling for the linear diapirism hypothesis. Turtle et al. have created a finite element model for the wedging hypothesis (Turtle et al. 1998); future modeling of the remaining other hypotheses would allow for a better comparison of the various ridge formation hypotheses.
Description of Model
A key point of the linear diapirism hypothesis is that it addresses a number of morphological features connected with the double ridges. The double ridges themselves are generally linear, long, and quite consistent in their dimensions along the length of the ridge. From space probe photos they have been measured to reach up to 300 meters in height, two and a half kilometers in width, and thousands of kilometers in length, having a side slope as steep as 12 degrees. There are dips on either side of the double ridges, called marginal troughs, which on 200m high ridges have been estimated by photoclinometry to be 10-20 meters deep. Just outside these marginal troughs are often found thin fractures that run roughly parallel to the ridge. The slopes of the ridges show evidence of mass wasting, with chutes where material has sloughed off. Also seen on the slopes are areas where the background ridges, overlaid with a new ridge, continue up the side of the new ridge. Examples of all these features can be seen in Figure 1.
Head et al. compares these features to smaller geologic features on Earth caused by salt diapirism, and points out that this diapirism on Europa would explain other Europan surface features including elliptical pits and domes. He suggests a two-layer model in which a cold, brittle layer of ice rests on top of a warmer, ductile ice layer. Stress fractures induced by diurnal tidal stresses and nonsynchronous rotation tidal stresses may reach into the ductile layer, and the friction along these fractures heats the surrounding ductile ice, which becomes more buoyant and pushes up the brittle surface ice slabs along the fracture. Rim synclines, folding caused by lateral forces from the initial opening of the crack and topography of the ridge, and flexure from the ridge load are all explanations pointed out for the marginal troughs under this model. Finally, during the deformation processes mass wasting of the steep ridge slopes would be expected as would the existence of previous ridges on the new slabs being lifted and deformed.
While an intricate numerical model that exactly fits the measured topography may not be appropriate at this early stage when so little is known about Europa's environment, a rough model based on the physics of the linear diapir hypothesis would be useful whether it turned out to match the measured topography or not. A match would support the linear diapir formation hypothesis, or if there is a poor match, this may suggest the hypothesis might require rethinking. In order to describe the features of the proposed numerical model, let us first look at a simple version and a few results from it.
Figure 2 shows a simple cantilever plate suspended with both its top and bottom surfaces free of normal and shear stresses. There is no gravity and no contacting material to apply stress to the plate; the only external force acting on this cantilever is the edge force pushing up at the very end of the plate. We can set up a mathematical description for this system in MKS units and solve for the displacement of the plate, relying on the assumption that the thickness of the plate is significantly smaller than its length.
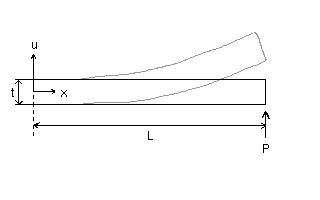
Figure 2. A very simple model for plate deformation to aid in discussing modeling approaches to substantiate the linear diapir hypothesis for Europan ice ridge formation.
First we obtain a force moment from the upward edge force P at the end of the plate:
ML = Px
Next, if we assume that the plate is elastic with flexural rigidity D then we can describe the force moment in a cross section of the plate in terms of the place's displacement:
![]()
We relate these two by a balance of moments, ML + Mt = 0, and obtain:
![]()
given the following definition for D with respect to the elastic modulus M, Young's modulus E, Poisson's ratio v, and thickness t of the plate.
![]()
We can integrate the second order differential equation above twice to obtain the displacement u(x) of the plate in response to the upward edge force, a cubic equation:
![]()
Then we can plug in reasonable values for E, v, P, and t, and plot it as seen in Figure 3 as seen below.
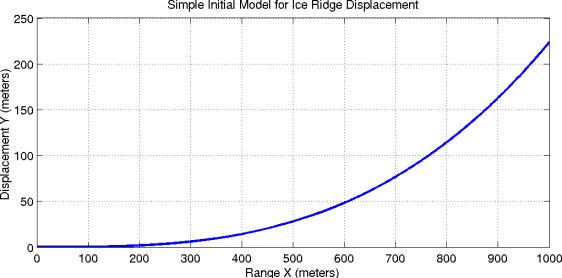
Figure 3. Plot of the solution for plate displacement u vs range x, given values of E=9.33*109 Pa, v=.325, P=5*107Pa, t=35m
The small model here is of course an extremely simplistic one. We do see that this plate bends upward in response to the edge force, with a height and slope of the order described in Head et al. 1999. The addition of a gravitational component may add a response in the displacement curve that matches the marginal troughs, similar to the response seen on the ocean floor as it rises first before descending into a subduction zone. All the variables except the edge force are based on “reasonable” values - Young's modulus E and Poisson's ratio v were taken from Chuang (2001) for polycrystalline ice at -16ºC, and ridge length L and thickness t are set to match the dimensions discussed in Head et al. 1999 regarding the linear diapir hypothesis. The upward edge force of 5*107 Pa, on the other hand, was merely chosen to make the displacement in the plot comparable to that in the measured ridge, and seems rather large. But as a single point force, presumably it stands in for a spread-out series of more realistically valued buoyancy forces caused by heat diffusion emanating from the fracture.
This heat diffusion would create both horizontal and vertical gradients in the buoyancy forces, significantly complicating the model. Other factors that would add insight to the model include exploring the effects of viscoelastic creep and analyzing the stability of the ridge slope (that is, at what points in its curvature it breaks, limiting which curvature solutions would remaining standing). In any case, keeping the model physically based, rather than attempting to merely fit it to measured data, is key.
The resulting model's displacement curves, given various tunings of its parameters, will then be compared to estimated 3D data of several Europan ridges, compiled by NASA/JPL/Caltech via photoclinometry of space probe photos. A successful model that matches the linear diapir formation hypothesis as well as the measured topography data would provide a platform for exploring parameters such as ice layer thickness and ice rigidity. If the model does not make for a good match between the linear diapir formation hypothesis and the estimated 3D data, then this information is also important as it helps in the narrowing down of applicable formation hypotheses. Ideally all the formation hypotheses might be explored numerically in the intermediate future, in separate projects, so that they can be better compared and evaluated.
References
Anderson, J. D., G. Schubert, R. A. Jacobson, E. L. Lau, W. B. Moore, W. L. Sjogren, Europa's Differentiated Internal Structure: Inferences from Four Galileo Encounters, Science, 281, 2019-2022, 1998.
Chuang, F.C., P. H. Figueredo, R. L. Kirk, and R. Greeley, Europa's 'Mitten': Estimate of Ice Thickness Using an Elastic Plate Model, Lunar and Planetary Science XXXII, 2001.
Gaidos, Eric J. and Francis Nimmo, Tectonics and water on Europa, Nature, 405, 637, 2000.
Head, James W. and Robert T. Pappalardo, Europa: Morphological characteristics of ridges and triple bands from Galileo data (E4 and E6) and assessment of a linear diapirism model, J. Geophys. Res., 104, 24223-24236, 1999.
Hobbs, Peter V., Ice Physics, Clarendon Press, Oxford, 1974.
NASA Planetary Photojournal, NASA/JPL/Caltech, http://photojournal.jpl.nasa.gov
Pappalardo, R. T., et al., Does Europa have a subsurface ocean? Evaluation of the geological evidence, J. Geophys. Res., 104, 24015-24055, 1999.
Turtle, E. P., H. J. Melosh, and C. B. Phillips, Tectonic modeling of the formation of Europan Ridges, (abstract), Eos Trans. AGU, 79, suppl., F541, 1998.
