Flow_models series: Overview / Introduction
- The examples in this series are all computed with the scripts in my https://github.com/aganse/flow_models repo in Github.
- Links to articles in the series (also in nav menu above): 0.) Overview / Intro, 1.) Distribution mapping, 2.) Generative image modeling / anomaly detection, 3.) Generative classification (a), 4.) Generative classification (b), 5.) Ill-conditioned parameter estimation, 6.) Ill-posed inverse problem ignoring noise, 7.) Ill-posed inverse problem with noise in the data
Normalizing-flow models are invertible neural networks (INNs) — a type of generative model that allows not only generating new samples from the learned distribution (which GANs and VAEs do too) but also exact likelihood computation as well (which GANs and VAEs do not). This is accomplished with an architecture that ensures all transformations are reversible and the Jacobian determinant is efficiently computable. By modeling probabilities directly, INNs allow for a range of other applications too - a real Swiss-army-knife of the modeling world that I'm recently fascinated with.
Other implementations of INNs I've seen out there only cover one specific application and with a lot of bespoke code. But the Tensorflow Probability package provides almost everything needed to implement these models in a more encapsulated, cleaner, and easier to understand way (at least for me!). Of course as I expand this work I'm wrestling a number of tradeoffs in what to generalize/simply via TFP and what to explicitly implement - part of the learning process for me.
The above diagram summarizes, for different applications, variations in how the N-dimensional model inputs are mapped through the flow model to N-dimensional outputs that include a latent multivariate standard normal distribution to capture some or all of the complex variations on the input side. All those output points can each be mapped back though the model to the inputs as well, important in the image generation, uncertainty quantification, and inverse problems among others. (The little images in each frame of the gif are subtle references to the example applications I'm implementing for each variation, and key research papers from the literature that describe these variations one at a time.)
By virtue of being bijective, these layers' Jacobians are square and invertible, which means their determinants are never zero. This allows the flow model's change-of-variables function to scale the volumes between the two spaces, mapping probability densities from one side's \(p_Z(z)\) to the other side's \(p_X(x)\):
Anyhow, so when one needs the likelihood of the data X, in trivial problems where one already knows the probabilities of the points in X (say they were random samples from a known Gaussian distribution), then one could compute their likelihood directly from those probabilities as:
So these normalizing-flow models give us a.) a one-to-one mapping to actual probabilities in the latent space corresponding to input points, b.) a way to compute the likelihood of the data exactly, and c.) really efficient computation that allows practical training time for complex models, as the Jacobians are not dependent on the arbitrarily complex layers inside the affine coupling layers.
1. Distribution mapping
2. Generative image modeling / anomaly detection
3. Generative classification (a)
4. Generative classification (b)
5. Ill-conditioned parameter estimation
6. Ill-posed inverse problem ignoring noise
7. Ill-posed inverse problem with noise in the data
1. RealNVP paper
2. NICE paper
3. Glow paper
Generative classification and ill-conditioned parameter estimation with INNs:
4. Ardizzone 2019 INNs paper
Bayesian inverse problems with INNs:
5. Zhang & Curtis 2021 JGR paper
TensorFlow Probability components:
6. tfp.bijectors.RealNVP API
- The examples in this series are all computed with the scripts in my https://github.com/aganse/flow_models repo in Github.
- Links to articles in the series (also in nav menu above): 0.) Overview / Intro, 1.) Distribution mapping, 2.) Generative image modeling / anomaly detection, 3.) Generative classification (a), 4.) Generative classification (b), 5.) Ill-conditioned parameter estimation, 6.) Ill-posed inverse problem ignoring noise, 7.) Ill-posed inverse problem with noise in the data
Normalizing-flow models are invertible neural networks (INNs) — a type of generative model that allows not only generating new samples from the learned distribution (which GANs and VAEs do too) but also exact likelihood computation as well (which GANs and VAEs do not). This is accomplished with an architecture that ensures all transformations are reversible and the Jacobian determinant is efficiently computable. By modeling probabilities directly, INNs allow for a range of other applications too - a real Swiss-army-knife of the modeling world that I'm recently fascinated with.
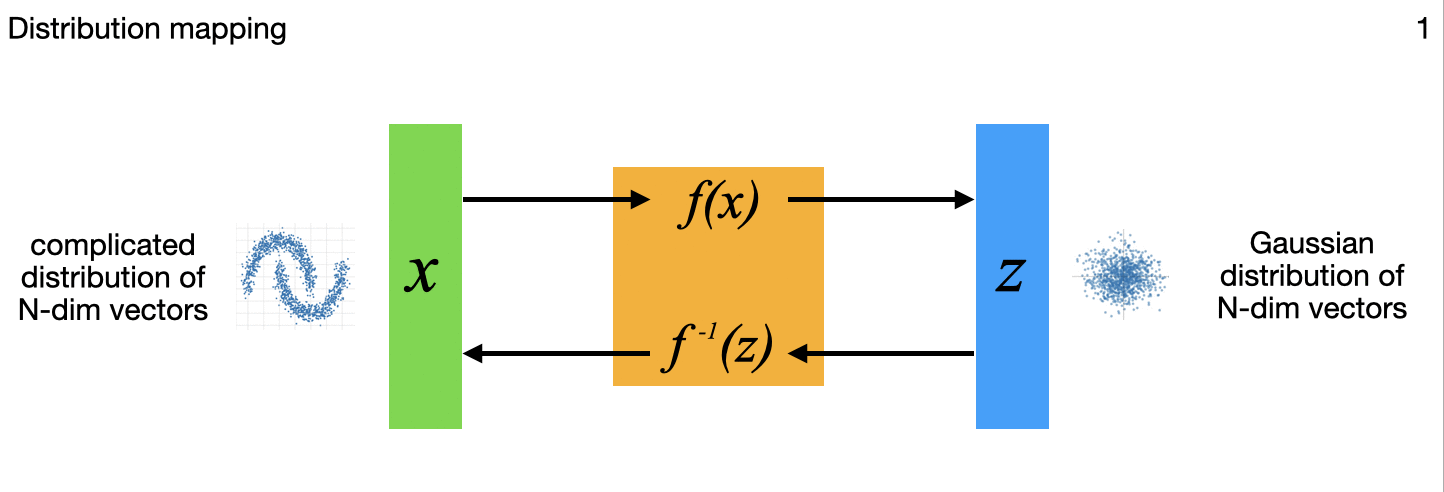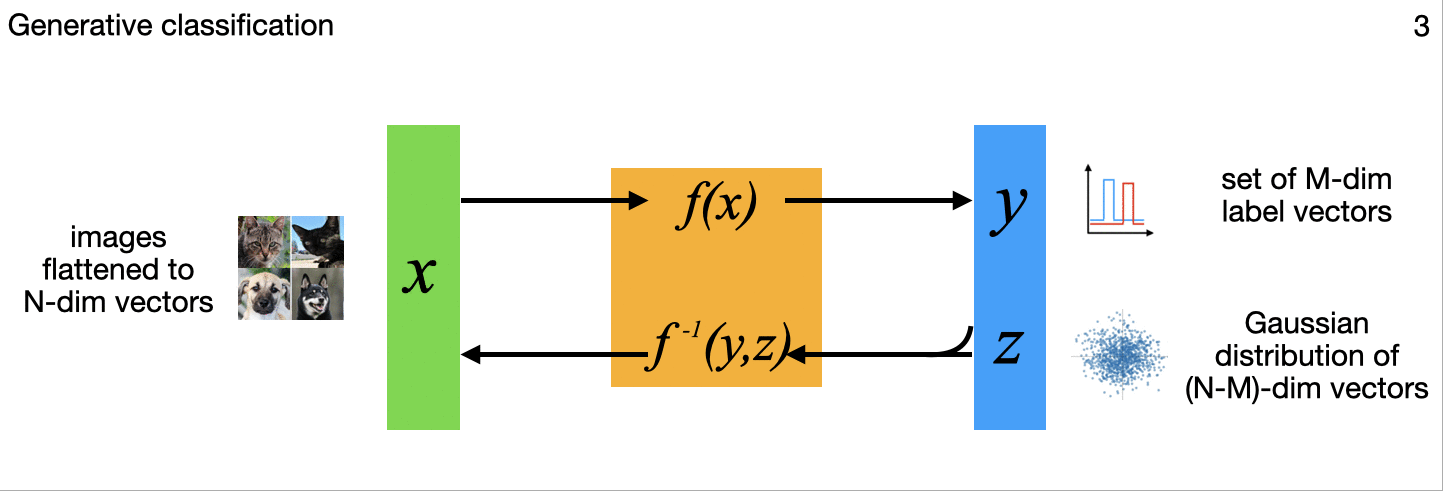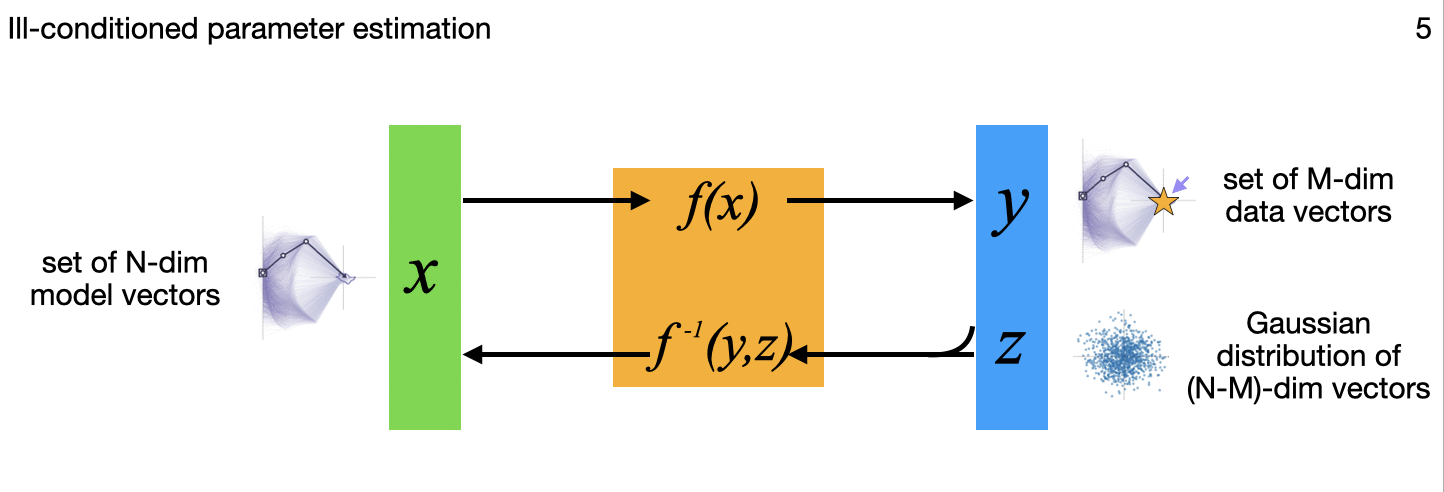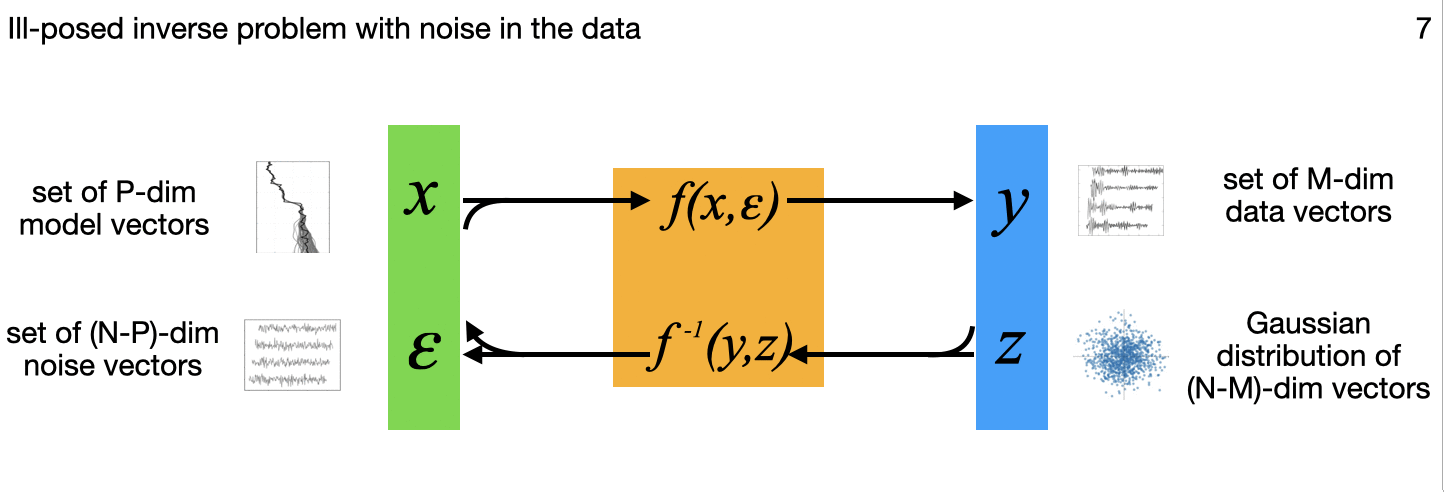 | frame: 1 2 3 4 5 6 7 ↻ |
Summary
These normalizing-flow models transform complex data distributions into more tractable ones (usually Gaussian) in which it's feasible to do probabilistic calculations such as anomaly detection for example. But these models allow far more than anomaly detection - their capabilities allow INNs to cover generative image modeling, generative classification, parameter estimation on ill-conditioned problems, and (ill-posed) inverse problems with or without noise on the data. All of these stem from the theme of mapping one probability distribution into another.Other implementations of INNs I've seen out there only cover one specific application and with a lot of bespoke code. But the Tensorflow Probability package provides almost everything needed to implement these models in a more encapsulated, cleaner, and easier to understand way (at least for me!). Of course as I expand this work I'm wrestling a number of tradeoffs in what to generalize/simply via TFP and what to explicitly implement - part of the learning process for me.
The above diagram summarizes, for different applications, variations in how the N-dimensional model inputs are mapped through the flow model to N-dimensional outputs that include a latent multivariate standard normal distribution to capture some or all of the complex variations on the input side. All those output points can each be mapped back though the model to the inputs as well, important in the image generation, uncertainty quantification, and inverse problems among others. (The little images in each frame of the gif are subtle references to the example applications I'm implementing for each variation, and key research papers from the literature that describe these variations one at a time.)
Brief technical description
The key to flow models is their bijectivity (reversibility). That's down at their layer level, referring to their "affine coupling layers", which one stacks to create a larger overall bijective INN. The bijectivity of these layers comes from a wonderfully clever approach where the layer splits the input, and on one part applies an affine transformation involving multiplication by the exponential of an arbitrarily complicated function (eg CNN layers etc). The other part just maps straight through, allowing the opposite arrangement for the reverse direction. The cleverness is that the inverse of the affine operation conveniently does not require the inverse of that arbitrarily complicated function, and similarly the Jacobian of this layer does not require the Jacobian of that arbitrarily complicated function. So it's a network layer that can be arbitrarily complicated, and also invertible, and also has a really efficient Jacobian. See details in the brief Section 3 of the RealNVP paper (linked at bottom of this page).By virtue of being bijective, these layers' Jacobians are square and invertible, which means their determinants are never zero. This allows the flow model's change-of-variables function to scale the volumes between the two spaces, mapping probability densities from one side's \(p_Z(z)\) to the other side's \(p_X(x)\):
\( p_X(x) = p_Z(f(x)) \cdot \left| \det\left(\frac{\partial f(x)}{\partial x}\right)\right| \)
Anyhow, so when one needs the likelihood of the data X, in trivial problems where one already knows the probabilities of the points in X (say they were random samples from a known Gaussian distribution), then one could compute their likelihood directly from those probabilities as:
\(\text{L} = \sum_{i=1}^n \log p_X(x_i)\)
So these normalizing-flow models give us a.) a one-to-one mapping to actual probabilities in the latent space corresponding to input points, b.) a way to compute the likelihood of the data exactly, and c.) really efficient computation that allows practical training time for complex models, as the Jacobians are not dependent on the arbitrarily complex layers inside the affine coupling layers.
This article series
This series of articles will implement and describe a set of modeling examples corresponding to the frames 1-7 above, a number of which come from some key research papers on INNs (listed at bottom). It's all the same model for all these applications, just with a few variations in the partitioning of the inputs and outputs. The first entry (which was actually article #2) comprised the bulk of the work, whereas the rest are variations using same modeling code so should come much more quickly. You'll see these gradually fill in over time:1. Distribution mapping
2. Generative image modeling / anomaly detection
3. Generative classification (a)
4. Generative classification (b)
5. Ill-conditioned parameter estimation
6. Ill-posed inverse problem ignoring noise
7. Ill-posed inverse problem with noise in the data
Key references
Distribution mapping and generative image modeling with INNs:1. RealNVP paper
2. NICE paper
3. Glow paper
Generative classification and ill-conditioned parameter estimation with INNs:
4. Ardizzone 2019 INNs paper
Bayesian inverse problems with INNs:
5. Zhang & Curtis 2021 JGR paper
TensorFlow Probability components:
6. tfp.bijectors.RealNVP API
